Правилото на дясната ръка: кръстосано произведение и посока на вектори
Правилото на дясната ръка: ясно и практично обяснение на кръстосаното произведение, стъпки, примери и как да определяте посоката при умножение на вектори.
Правилото на дясната ръка е удобна конвенция в областта на векторната математика, която помага да се определи посоката на резултата от кръстосано (векторно) произведение на два вектора.
Основна идея: когато вземете кръстосано произведение a × b, резултатът е вектор, който е перпендикулярен както на a, така и на b, а посоката му се определя чрез правилото на дясната ръка.
- Поставете дланта на дясната си ръка така, че да можете да движите пръстите от първия вектор към втория.
- Протегнете показалеца си в посоката на първия вектор (a).
- Протегнете палеца си в посоката на втория вектор (b), като свиете ръката в китката така, че показалецът и палецът да са приблизително под прав ъгъл.
- Средният ви пръст (или указателен в някои варианти) ще сочи в посоката на кръстосаното произведение a × b.
По-просто казано: насочете палеца си в посоката на първия вектор и показалеца си в посоката на втория вектор; средният пръст ще показва посоката на кръстосаното произведение. Това е и удобен визуален начин за бърза проверка при задачи с три измерения.
Стъпка по стъпка (алтернативен, често показван начин):
- Затворете дясната си ръка и изпънете показалеца;
- Вдигнете палеца си нагоре (като правите „пистолет“);
- Изпънете средния пръст така, че показалецът, палеца и средният пръст да са по три взаимно перпендикулярни оси.
Важно свойство: когато смените реда на векторите, посоката се обръща: a × b = −(b × a). Също така, ако двата вектора са паралелни или антипаралелни, кръстосаното произведение е нулев вектор.
Магнитуда на кръстосаното произведение: |a × b| = |a| |b| sin(θ), където θ е ъгълът между векторите a и b. Това означава, че модулът на резултата зависи от големината на векторите и от синуса на ъгъла между тях (максимален е при θ = 90°).
Свойства и приложения:
- Резултатът е ортогонален (перпендикулярен) на двата множителя;
- антикомутативност: a × b = −b × a;
- разпределителност спрямо събиране: a × (b + c) = a × b + a × c;
- широко приложение в физиката: магнитни сили, момент на сила (момент/торк), ъглов импулс и др.
Пример в картезиански координати: ако e_x, e_y и e_z са стандартните единични вектори, то e_x × e_y = e_z, e_y × e_z = e_x, и e_z × e_x = e_y. Това следва директно от правилото на дясната ръка и определя ориентацията на десния координатен базис.
Изчисляване по компоненти: за вектори a = (a_x, a_y, a_z) и b = (b_x, b_y, b_z) компонентите на a × b се намират чрез „детерминант“ на матрица или чрез формулите
- (a × b)_x = a_y b_z − a_z b_y
- (a × b)_y = a_z b_x − a_x b_z
- (a × b)_z = a_x b_y − a_y b_x
Мнемоники: освен описания горе вариант, има и друг често използван начин — поставете дясната си ръка така, че показалецът да сочи в посоката на първия вектор, средният — в посоката на втория, а палеца автоматично ще посочи вектора на резултата (в зависимост от използваната постановка на пръстите).
Запомнете също, че когато промените реда на кръстосано умножение на векторите, резултатът ще бъде в обратна посока. Затова е важно да се уверите, че преминавате в реда t h u m b → × p o i n t e r → = m i d d l e → {\displaystyle {\vec {thumb}}\times {\vec {pointer}}={\vec {middle}} 
Ако искате, мога да добавя кратки визуални примери или малка задача с решение, за да упражните правилото на дясната ръка.

Правило на дясната ръка за движение, произведено с винтови резби

Ориентацията за лява ръка е показана отляво, а за дясна ръка - отдясно.
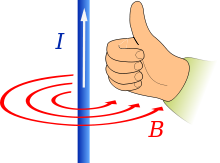
Предсказване на посоката на полето (B), когато токът I тече по посока на палеца
Вариации
Съществува и друго правило, наречено правило на дясната ръка (или правило на винта), което се използва за магнитни полета и неща, които се въртят.
1. Започнете, като изпънете дясната си ръка и насочите палеца си право навън, така че да е под прав ъгъл спрямо останалите пръсти.
2. Сега свийте пръстите си в юмрук и дръжте палеца си навън (като при палец нагоре).
3. Съобразете начина, по който пръстите ви се свиват, с начина, по който се движи нещо. Посоката, в която сочи палецът ви, е посоката на вектора, който използваме, за да говорим за него.
Можете да направите това и в обратна посока, като започнете с палеца си по посока на вектора и видите как се свиват пръстите ви, за да видите посоката на въртене. Ако насочите палеца си в посоката на тока в проводник, магнитното поле, което се появява около него, е в посоката на свиване на пръстите ви.
Въпроси и отговори
В: Какво представлява правилото на дясната ръка?
О: Правилото на дясната ръка е конвенция във векторната математика, която ви помага да запомните посоката, когато векторите се умножават кръстосано.
В: Как се използва правилото на дясната ръка, за да се разбере посоката на кръстосано произведение?
О: За да разберете посоката на кръстосано произведение, затворете дясната си ръка и изпънете показалеца си. Изпънете палеца си право нагоре, сякаш правите знак за пистолет. Насочете "пистолета" право напред, след това изпънете средния си пръст така, че да сочи наляво и всички пръсти да са под прав ъгъл един спрямо друг. Насочете палеца си по посока на първия вектор, а показалеца - по посока на втория вектор. Средният ви пръст ще сочи по посока на кръстосаното произведение.
Въпрос: Какво се случва, ако смените реда при кръстосаното умножение на векторите?
О: Когато смените реда на кръстосано умножение на векторите, резултатът отива в противоположни посоки. Затова е важно да се уверите, че вървите в реда палец х показалец = среден .
В: Какво означава това уравнение? {\displaystyle {\vec {thumb}}\times {\vec {pointer}}={\vec {middle}}} .
О: Това уравнение означава, че ако два вектора се пресекат, умножени един с друг (палец х показалец), ще се получи трети вектор (middle).
обискирам