Лавинен ефект в криптографията: дефиниция, значение и примери
Ефектът на лавината ("ефект на свлачището") е важна характеристика на блоковите шифри и алгоритмите на криптографските хеш функции. Той е желано свойство в практическата криптографията, тъй като гарантира, че малка промяна във входа води до голяма и неочаквана промяна в изхода. Конкретно, при добрите блокови шифри малка промяна в ключа или в открития текст трябва да предизвика значителна и широко разпространена промяна в шифровия текст, така че отделните битове на шифровия текст да зависят от много битове на входа.
Ефектът означава също така, че малки промени се разпространяват бързо, когато алгоритъмът използва многократни итерации. В идеалния случай всеки бит от изхода зависи по комплексен начин от всеки бит от входа, така че информацията за входа да не може да бъде възстановена от изхода без познаване на ключа или вътрешната структура.
Терминът "лавинен ефект" е използван за първи път от Хорст Файстел (Feistel 1973). По-късно понятието е идентифицирано със свойството на объркване на Шанън, което заедно с дифузията формира основните принципи при проектиране на сигурни криптосистеми.
Формална дефиниция и критерии
В по-строг смисъл лавинният ефект се дефинира така: при промяна на един бит от входа се очаква приблизително половината от битовете на изхода да се променят. Този праг от ~50% е целево поведение за да се постигне максимална рандомизация. Оттук произлизат и някои формализирани критерии:
- Strict Avalanche Criterion (SAC) — за всяка входна промяна от един бит вероятността всеки изходен бит да се промени е 50%.
- Bit Independence Criterion (BIC) — промените в различни изходни битове трябва да бъдат статистически независими при промяна на единичен входен бит.
Как се измерва ефектът на лавината
Практическите тестове използват експериментални подходи:
- Извършва се множество изпълнения на алгоритъма с входове, различаващи се само в един бит, и се измерва Хамингова дистанция между съответните изходи. Средната стойност трябва да бъде близка до половината от дължината на изхода.
- Статистически тестове за равномерност, независимост и корелация между битовете на изхода.
- Анализи за устойчивост спрямо диференциален и линейен криптоанализ — добър лавинен ефект затруднява откриването на предсказуеми вход-изход зависимости.
Примери и практическо значение
Много модерни алгоритми се стремят към силен лавинен ефект. Например, при добре проектиран блоков шифър след няколко рунда една малка промяна в открития текст трябва да промени приблизително половината битове на шифровия текст. При криптографските хеш функции като SHA-2 и SHA-3 аналогично — една малка промяна в съобщението води до голяма промяна в хеша, което прави предсказването и колизиите по-трудни.
Защо е важно за сигурността
- Предотвратява лесно възстановяване на информация за входа от изхода — липсата на лавинен ефект дава структурни уязвимости.
- Увеличава устойчивостта към диференциални атаки — ако малки промени не се разпространяват добре, атакуващият може да проследи относително предвидим маршрут на разсейване на разликите.
- Подобрява непредсказуемостта на изхода, което е критично за криптографския дизайн и за функции за проверка на целостта.
Ограничения и допълнителни изисквания
Важно е да се отбележи, че силният лавинен ефект сам по себе си не гарантира пълна сигурност. Той е необходим, но не и достатъчен признак за добър дизайн. Други свойства като нелинейност, устойчивост към специфични атаки, липса на лесни математически зависимости и обща криптографска здравина също са критични. В практиката дизайнът обединява концепциите на Шанън — объркване и дифузия — за да постигне както лавинен ефект, така и други желани характеристики.
Какво да търсим при оценка
- Колко рунда са необходими, за да се постигне близко до 50% изменение на разпределението на битовете.
- Резултати от емпирични тестове (Хамингова дистанция, SAC, BIC).
- Анализи от криптоанализатори и устойчива история на алгоритъма в реални приложения.
В обобщение, ефектът на лавината е ключово свойство за сигурни криптографски примитиви: той гарантира, че малките промени в данните или ключа довеждат до големи, непредсказуеми промени в изхода, което усложнява анализа и атаките върху алгоритъма.
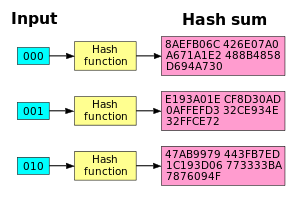
Функцията за хеширане SHA1 има добър лавинообразен ефект. При промяна на един-единствен бит сумата на хеша става напълно различна.
Име
Произходът на името е от свлачища. Малък камък може да падне, да се свлече заедно със сняг и да образува разрушително свлачище. Скалата е малка, но може да причини много разрушения. Това е същото, което прави този ефект. Малка промяна на входа (скалата) трябва да промени изхода (ландшафта).
Строг критерий за лавина
Строгият критерий на лавината (SAC; "критерий на силното свлачище") е свойство на булевите функции. То е от значение за криптографията. Той е изпълнен, ако всички изходни битове се променят с вероятност 50 %, ако се промени един единствен входен бит.
ВАК е изградена върху концепциите за пълнота на еволюцията и лавинообразност. Тя е въведена от Уебстър и Таварес през 1985 г. В днешно време тя е изискване за всяка съвременна криптографска система. То е изпълнено например от всички финалисти на състезанието AES.
Критерий за независимост на бита
Критерият за независимост на бита (BIC; критерий, независим от бита) е критерий. Той гласи: Когато един входен бит се промени (инвертира), два изходни бита трябва да се променят независимо един от друг. Това се отнася за всички битове.
Тя например няма да бъде удовлетворена, ако единият изходен бит се променя само когато се променя и другият изходен бит. Те могат да се променят само защото входният бит се е променил. В противен случай изходните битове ще зависят един от друг.
Свързани страници
- Объркване и разпространение
Въпроси и отговори
В: Какво представлява лавинният ефект?
О: Ефектът на лавината (известен също като "ефект на свлачището") е свойство на блоковите шифри и алгоритмите на криптографските хеш-функции, което гласи, че малка промяна в ключа или в открития текст трябва да предизвика силна промяна в шифровия текст.
Въпрос: Кой пръв използва термина "лавинен ефект"?
О: Терминът "лавинен ефект" е използван за първи път от Хорст Файстел през 1973 г.
Въпрос: Как се отнася към свойството на Шанън за объркване?
О: Концепцията за лавинообразния ефект е идентифицирана чрез свойството на объркване на Шанън, което гласи, че ако блоков шифър или криптографска хеш функция не удовлетворява тази степен в значителна степен, то тя има лоша рандомизация и може да бъде частично или напълно разбита (кракната).
Въпрос: Какви са някои цели на проектирането при създаването на силни шифри?
О: Когато хората създават силни шифри, те се опитват да вградят в тях добър лавинообразен ефект, като използват математически принципи като ефекта на пеперудата. Ето защо повечето блокови шифри са продуктови шифри и защо хеш-функциите имат големи блокове данни.
Въпрос: Какво се случва, ако даден алгоритъм не удовлетворява ефекта на лавината?
О: Ако даден алгоритъм не удовлетворява ефекта на лавината в значителна степен, тогава той има лоша рандомизация и може да бъде частично или напълно разбит (разбит) от криптоаналитици, които могат да правят прогнози за входа само въз основа на дадения изход.
Въпрос: Защо повечето блокови шифри използват продуктови шифри?
О: Повечето блокови шифри използват продуктови шифри, защото те помагат да се вградят в тях добри ефекти на авалиране, като се използват математически принципи като ефекта на пеперудата.
В: Защо хеш-функциите имат големи блокове данни?
О: Хеш-функциите имат големи блокове от данни, защото това помага за изграждането на добри ефекти на авалиране в тях, като се използват математически принципи като ефекта на пеперудата.
