Теорема на Холанд за схеми: определение, значение и критичен преглед

Изчерпателно обяснение на Теоремата на Холанд за схеми — дефиниция, значение за генетичните алгоритми и критичен преглед на ограниченията и интерпретациите.

Автор: Leandro Alegsa

01-09-2025 21:31

Схематичната теорема на Холанд, наричана още фундаментална теорема на генетичните алгоритми, е неравенство, получено чрез приближено структуриране на уравнение за еволюционна динамика на популация от решения. Теоремата за схемите формулира, че кратките схеми от нисък порядък с пригодност над средната имат тенденция да увеличават относителната си честота в следващите поколения при стандартните оператори на селекция, кръстосване и мутация. Тя е предложена от Джон Холанд през 70-те години на XX в. и първоначално е била възприемана като основа за обяснение на ефективността на генетичните алгоритми. Това тълкуване впоследствие е подложено на критика в литературата: в няколко публикации е показано, че схемната теорема може да се разглежда като частен случай на по-общи формулировки (например уравнението на Прайс), когато се използва индикаторната функция на схемата като агрегираща мярка.

Дефиниции и нотация

За да се разбере по-добре съдържанието на теоремата, въведете някои основни понятия:

Схема (schema) H: шаблон над азбука (обикновено {0,1} при бинарни низове), съдържащ фиксирани символи и „дива“ позиции обозначавани с *, които не са фиксирани. Схемата определя подмножество от низове, които съвпадат с фиксираните позиции.
Дължина на низовете l: брой позиции в хромозомата (низовете).
Поръчка на схемата o(H): брой фиксирани позиции в H.
Дефинираща дължина δ(H): разстоянието (индексна разлика) между първата и последната фиксирана позиция в H.
m(H,t): брой индивиди в популацията на поколение t, които съвпадат със схемата H.
f(H): средна пригодност на всички индивиди, които съвпадат със схемата H; f̄ (f-bar) е средната пригодност на цялата популация.
p_c и p_m: вероятности за кръстосване и за единична битова мутация (или съответни оператори за други възможни представяния).

Формулировка на теоремата (интуитивно и формално)

Интуитивно: ако дадена схема H има средна пригодност над средната за популацията (f(H) > f̄), кратка дефинираща дължина и малък порядък (малко фиксирани позиции), то под влиянието на селекцията, и при условие че операторите за вариация не я разрушават твърде често, относителният брой на екземплярите на H в следващото поколение ще се увеличи.

Една стандартна (приближена) форма на неравенството, дадена в класическата литература, е:

E[m(H,t+1)] ≥ m(H,t) * (f(H) / f̄) * [1 - p_c * (δ(H) / (l-1))] * (1 - p_m)^{o(H)}

Тук:

първият множител m(H,t) представлява настоящия брой екземпляри на схемата;
факторът (f(H) / f̄) отразява очаквания ефект на селекцията (над средната пригодност води до растеж);
факторът [1 - p_c * (δ(H) / (l-1))] е приближение за вероятността, че едно случайно едноточково кръстосване няма да раздели схемата (зависи от дефиниращата дължина);\
(1 - p_m)^{o(H)} е вероятността, че нито една от фиксираните позиции не бъде променена от мутация (за малки p_m често се използва линейното приближение 1 - o(H)p_m).

Пример

Нека имаме бинарни низове с дължина l = 6 и схема H = 1 * 0 * * 1 (фиксирани позиции 1,3,6). Тогава o(H)=3 и δ(H)=6-1=5. Ако p_c е високо и δ(H) е голяма, схема H е лесно разрушима от кръстосване. Ако обаче H има средна пригодност значително над f̄ и p_m е малка, броят на екземплярите m(H,t) ще има тенденция да расте за няколко поколения според теоремата.

Значение и интерпретация

Схемната теорема подчертава ролята на кратките, нископорядкови „строителни блокове“ като градивни елементи в хипотезата за building blocks: добри локални комбинации от гени биват селектирани и съчетавани за изграждане на по-добри решения.
Теоремата показва как селекцията насърчава увеличаването на честотата на надсредно пригодни схеми, стига операторите за вариация да не ги разрушават често.
В педагогичен смисъл тя дава аналитична връзка между пригодността и вероятността за оцеляване на структурни характеристики (схеми) в популация.

Критичен преглед и ограничения

Въпреки своята влиятелност, схемната теорема има редица важни ограничения и е била подлагана на критика:

Не е еквивалент на прогноза за практическа работа: теоремата дава долна граница (неравенство) за очаквания брой екземпляри и не гарантира, че дадена схема реално ще доминира при практическо изпълнение — в игра влизат статистическа флуктуация, стохастични ефекти и баланс между разрушаване и създаване на схеми.
Игнорира създаването на схеми: класическата формула разглежда предимно запазването (survival) на съществуващите екземпляри и не отчита подробно колко нови екземпляри на дадена схема може да бъдат създадени чрез кръстосване и мутация от други схеми.
Приема независимост и прост модел на операторите: например при едноточково кръстосване факторът за разрушаване е приближителен; при сложни оператори или представяния (небинарни, декодиране и т.н.) простите оценки могат да бъдат неточни.
Липса на цялостно обяснение: че кратките нископорядкови схеми растат при селекция не обяснява защо генетичният алгоритъм намира глобално добри решения; винаги остава въпросът как се комбинират и пазят по-големи структурни единици във времето.
Критики към „имплицитния паралелизъм“: Холанд и последователи формулират идеята, че един индивид експонира множество схеми едновременно (implicit parallelism). Някои изследователи оспорват количествената значимост на този аргумент за реални задачи и популации с ограничен размер.

Връзка с уравнението на Прайс

По-общи математически формулировки на еволюционните промени в агрегирани характеристики на популацията могат да бъдат дадени чрез уравнението на Прайс. В този контекст схемната теорема може да се интерпретира като специален случай на Прайс, когато като макроскопична характеристика се вземе индикаторната функция за принадлежност към дадена схема (т.е. стойност 1 за индивиди, които съвпадат със схемата, и 0 за останалите). Тази връзка показва, че схемната теорема не е „магически“ закон, а приложение на общи принципи на еволюционната динамика към специфична агрегираща функция.

Съвременни гледни точки и доработки

Разработени са по-прецизни (и по-общи) версии на схемната теорема, които включват вероятностен анализ, отчитащ създаването на схеми и корелациите между позиции.
Маркови модели и симулации дават точни прогнози за динамиката на популациите при конкретни настройки и размери на популацията.
В практиката критични са представянето (encoding), операторите и размера на популацията — затова дизайнерите на алгоритми използват хибридни подходи и адаптивни оператори, вместо да разчитат единствено на „строителни блокове“.

Заключение

Теоремата на Холанд за схемите е важна илюстрация на това как селекцията и операторите за вариация влияят върху честотите на структурни характеристики в генетичните алгоритми. Тя дава полезна интуиция за ролята на кратките, нископорядкови шаблони, но има ограничена прогностична сила сама по себе си. За модерния анализ на еволюционни алгоритми се използват по-общи и по-точни математически инструменти, комбинирани със симулации и емпирични тестове.

Схемите са формално шаблони, които идентифицират подмножество от низове със сходства в определени позиции. Те също така представляват специален случай на цилиндрични множества и по този начин формират топологично пространство, което позволява да се използват инструменти от теорията на множествата и топологията при формализиране на техните свойства.

Описание

Разглеждаме двоични низове с дължина 6. Схемата 1*10*1 описва множеството от всички низове с дължина 6 с 1 на позиции 1, 3 и 6 и 0 на позиция 4. Символът * е заместващ символ, което означава, че позиции 2 и 5 могат да имат стойност 1 или 0. Редът на една схема o ( H ) {\displaystyle o(H)} $o(H)$ се определя като броя на фиксираните позиции в шаблона, докато определящата дължина δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ е разстоянието между първата и последната специфична позиция. Редът на 1*10*1 е 4, а определящата му дължина е 5. Пригодността на дадена схема е средната пригодност на всички низове, съответстващи на схемата. Фитнесът на даден низ е мярка за стойността на кодираното решение на проблема, изчислена чрез специфична за проблема функция за оценка. Като се използват утвърдените методи и генетични оператори на генетичните алгоритми, теоремата за схемата гласи, че кратките схеми от нисък ред с фитнес над средния се увеличават експоненциално в последователните поколения. Изразено като уравнение:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Тук m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ е броят на низовете, принадлежащи към схема H {\displaystyle H} $H$ в поколение t {\displaystyle t} $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ е наблюдаваната средна пригодност на схема H {\displaystyle H} $H$ , а a t {\displaystyle a_{t}} $a_{t}$ е наблюдаваната средна пригодност в поколение t {\displaystyle t} $t$ . Вероятността за разрушаване p {\displaystyle p} $p$ е вероятността кръстосването или мутацията да разрушат схемата H {\displaystyle H} $H$ . Тя може да бъде изразена по следния начин:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

където o ( H ) {\displaystyle o(H)} $o(H)$ е редът на схемата, l {\displaystyle l} $l$ е дължината на кода, p m {\displaystyle p_{m}} $p_{m}$ е вероятността за мутация, а p c {\displaystyle p_{c}} $p_{c}$ е вероятността за кръстосване. Така че схема с по-малка дефиниционна дължина δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ е по-малко вероятно да бъде нарушена.
Често неразбираем момент е защо Теоремата за схемата е неравенство, а не равенство. Отговорът всъщност е прост: Теоремата пренебрегва малката, но ненулева вероятност низ, принадлежащ към схемата H {\displaystyle H} $H$ , да бъде създаден "от нулата" чрез мутация на един низ (или рекомбинация на два низа), който не е принадлежал към H {\displaystyle H} $H$ в предишното поколение.

Ограничение

Теоремата за схемите е валидна при предположението за генетичен алгоритъм, който поддържа безкрайно голяма популация, но невинаги се пренася в (крайната) практика: поради грешка при вземането на проби в началната популация генетичните алгоритми могат да се слягат със схеми, които нямат селективно предимство. Това се случва по-специално в мултимодалната оптимизация, където функцията може да има множество върхове: популацията може да се отклони, за да предпочете един от върховете, игнорирайки останалите.

Причината, поради която теоремата за схемата не може да обясни силата на генетичните алгоритми, е, че тя важи за всички случаи на проблеми и не може да направи разлика между проблеми, при които генетичните алгоритми се справят слабо, и проблеми, при които генетичните алгоритми се справят добре.

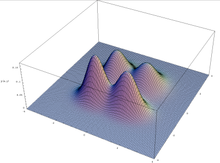
Построяване на мултимодална функция в две променливи.

Въпроси и отговори

Въпрос: Какво представлява теоремата на Холанд за схемите?

О: Теоремата за схемата на Холанд е теорема за генетичните алгоритми, която гласи, че индивидите с фитнес, който е по-висок от средния, е по-вероятно да надделеят.

В: Кой и кога е предложил теоремата за схемата на Холанд?

О: Джон Холанд предлага теоремата за схемата на Холанд през 70-те години на миналия век.

В: Какво е схема в контекста на генетичните алгоритми?

О.: В контекста на генетичните алгоритми схемата е шаблон, който идентифицира подмножество от низове със сходства в определени позиции на низовете.

В: Каква е интерпретацията на теоремата за схемата на Холанд, която се използва като основа за обяснения на силата на генетичните алгоритми?

О: Интерпретацията на теоремата за схемата на Холанд, която е използвана като основа за обяснение на силата на генетичните алгоритми, е, че индивидите с фитнес, който е по-висок от средния, е по-вероятно да надделеят.

Въпрос: Какво показаха критиките към теоремата за схемата на Холанд?

О: Критиката на теоремата за схемата на Холанд показа, че тя е специален случай на уравнението на Прайс, в което функцията на индикатора на схемата е макроскопичното измерване.

В: Кой е специалният случай на цилиндричните множества?

О: Схемите са специален случай на цилиндричните множества.

В: Какъв вид пространство образуват схемите?

О: Схемите образуват топологично пространство.

обискирам