Теория на Ейлер–Бернули за гредите — класическа инженерна дефиниция

Ясно обяснение на теорията на Ейлер–Бернули за греди: класическа инженерна дефиниция, формули и приложения при огъване, малки деформации и конструктивен дизайн.

Теорията на Ейлер–Бернули за гредите (често наричана и инженерна теория на гредите или класическа теория на гредите) дава опростен и практичен начин за изчисляване на огъването и вътрешните напрежения в извитата ос (гредата) при приложен товар. Тя се прилага при малки деформации и при допускането, че ефектите от срязващите деформации са пренебрежими; поради това е частен случай на по-общата теория на гредите на Тимошенко. Теорията е формулирана през XVIII в. и придобива широка популярност по време на индустриалната епоха — например при проектирането на структурни елементи като тези в Айфеловата кула и виенското колело в края на XIX век. Оттогава тя намира приложение в много области на инженерни дейности, включително в машиностроенето и гражданското строителство, и въпреки развитието на по-усъвършенствани модели остава широко използвана заради своята простота и ясни допускания.

Основни допускания

• Материалът е линейно-еластичен, хомогенен и изотропен (Hooke-ово поведение).
• Перфектно свързани секции: плоскостите, които са плътни преди огъване, остават плоски и перпендикулярни на неутралната ос след огъване (plane sections remain plane and normal).
• Срязването и въртящата инерция са пренебрежими — тоест огъването доминира; това прави модела невалиден за къси, дебели греди или при високи честоти.
• Деформациите са малки: геометричните нелинейности (големи завъртания или големи изкривявания) не се отчитат.
• Сечение със стабилни геометрични характеристики (момент на инерция I и модул на еластичност E са постоянни по дължината, освен ако не е указано друго).

Основно уравнение

В най-простия, едномерeн случай вертикалната отклонение w(x) на греда под разпределена сила q(x) удовлетворява четвъртопроизводното диференциално уравнение:

E I d^4 w / dx^4 = q(x),

където E е модулът на еластичност, а I — вторият момент на инерция на сечението. Връзката между огъващия момент M(x) и изкривяването е

M(x) = - E I d^2 w / dx^2.

Тези уравнения се използват за намиране на разпределението на огъване, ъглите на завъртане и вертикалните отклонения при дадени гранични условия.

Гранични условия и типични случаи

• Зададена стойност на изместване (закрепване): w = 0 (задържано), обикновено с нулев ъгъл при закачане (dw/dx = 0).
• Свободен край: моментът и срязващата сила са нулеви (M = 0, V = 0) — което води до d^2w/dx^2 = 0 и d^3w/dx^3 = 0.
• Просто поддържано (опряно): w = 0, но ротацията е свободна (M не е нула задължително).

Чрез комбиниране на уравненията и граничните условия се получават аналитични решения за стандартни натоварвания (напр. единично концентрирано натоварване, равномерно разпределен товар, момент) и типове опори.

Примери и приложения

• Изчисляване на статични огъвания и напрежения в греди в конструкции на сгради, мостове, машини и механични рамки.
• Бърза проверка при проектиране и оптимизация, когато допусканията са валидни.
• Изходна точка за числени методи (например метод на крайните елементи), където класическата теория дава референтни решения и гранични случаи.
• Свързана е и с критичното натоварване при издърпване (флексионно огъване на стълбове): формулата на Ойлер за критично натоварване P_cr = π^2 E I / (K L)^2 (където K е коефициент за ефективна дължина, L — дължина на колоната) се извежда в рамките на тази теория.

Ограничения и модерни алтернативи

Теорията не отчита значими срезови деформации и въртяща инерция — затова за къси и дебели греди, или при високи честоти на трептене, се използват по-сложни модели като теорията на Тимошенко (Timoshenko beam theory) или пълни триизмерни модели на линейна/нелинейна еластичност. За материално несъвършени, анизотропни или нехармонични сечения също са необходими разширения.

Практически съвети

• Преди да приложите формулите на Ейлер–Бернули, проверете дали гредата удовлетворява допусканията (отношение дължина/височина, малки деформации, линейна еластичност).
• При несигурност сравнете резултатите с по-точен числен модел (FEM) или използвайте корекционни фактори за срезови ефекти.
• За динамични задачи и високочестотни режими използвайте модели, които включват инерционни и срезови термини.

Заключение: Теорията на Ейлер–Бернули остава фундаментален и практически инструмент в инженерната практика за анализа на огъване на греди. Тя дава бързи и често достатъчно точни оценки при правилно приложение, но трябва да се използва с внимание към своите предпоставки и граници на приложимост.

История

Леонхард Ойлер и Даниел Бернули са първите, които създават теорията през 1750 г. По онова време на науката и техниката се гледа по различен начин, отколкото днес. Математически теории като теорията за лъча на Ойлер-Бернули не са се ползвали с доверие за практическа инженерна употреба. Мостовете и сградите продължават да се проектират по същите методи до края на XIX век. Тогава Айфеловата кула и виенското колело показват валидността на теорията в по-голям мащаб.

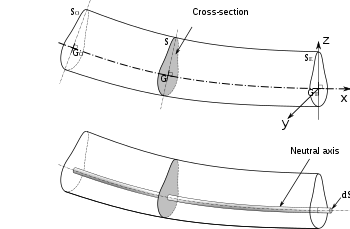
Чертеж на напречно сечение на огъната греда, показващо неутралната ос

Уравнение на статичната греда

Уравнението на Ойлер-Бернули описва връзката между деформацията на гредата и приложеното натоварване, както е показано по-долу:

d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}\right)=q\,}

Където w ( x ) {\displaystyle w(x)} описва деформацията на гредата в посока z {\displaystyle z} в някакво положение x {\displaystyle x} . q {\displaystyle q} е разпределен товар, с други думи сила на единица дължина (аналогично на налягането, което е сила на площ); той може да бъде функция на x {\displaystyle x} , w {\displaystyle w}. или други променливи.

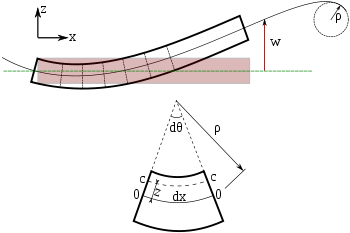
Огъване на греда на Ойлер-Бернули. Всяко напречно сечение на гредата е разположено на 90 градуса спрямо неутралната ос.

Въпроси и отговори

Въпрос: Какво представлява теорията за лъчите на Ойлер-Бернули?

Въпрос: Кога за първи път е въведена теорията на Ойлер-Бернули за гредите?

Въпрос: Използвана ли е теорията за гредата на Ойлер-Бернули при разработването на Айфеловата кула и виенското колело?

Въпрос: Кои са някои инженерни области, в които е използвана теорията за гредата на Ойлер-Бернули?

В: Широко ли се използва теорията на Ойлер-Бернули и днес?

Въпрос: За какви видове деформации на гредите се прилага теорията на Ойлер-Бернули?

Въпрос: Отчита ли теорията на Ойлер-Бернули ефекта на деформациите на срязване?

Търсене по буква