Закон на Снелиус
Законът за пречупване на Снел е научен закон за пречупването на светлината или други вълни. В оптиката законът на Снел се отнася до скоростта на светлината в различни среди. Законът гласи, че когато светлината преминава през различни материали (например от въздух към стъкло), съотношението на синусите на ъгъла на падане (влизане) и ъгъла на пречупване (излизане) не се променя:
sin θ 1 sin θ 2 = v 1 v 2 = n 2 n 1 {\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}} 
С всеки θ {\displaystyle \theta }
е ъгълът, измерен от нормалата на границата, v {\displaystyle v}
е скоростта на светлината в съответната среда (единиците на SI са метри в секунда или m/s). n {\displaystyle n}
е показателят на пречупване на средата.
Индексът на пречупване на вакуума е 1, а скоростта на светлината във вакуум е c {\displaystyle c}
. Когато вълна премине през материал, чийто показател на пречупване е n, скоростта на вълната става c n {\displaystyle {\frac {c}{n}}} 
.
Законът на Снел може да бъде доказан чрез принципа на Ферма. Принципът на Ферма гласи, че светлината се движи по пътя, който отнема най-малко време.
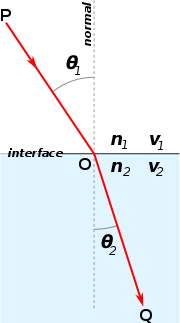
Пречупване на светлината на границата между две среди с различни показатели на пречупване, като n2 > n1
Светлинен лъч попада в стъклена призма и се пречупва
История
Тази идея има дълга история. Проблемът е бил обект на вниманието на Херо от Александрия, Птолемей, Ибн Сал и Хюйгенс. Ибн Сахл всъщност открива закона за пречупването. В "Traité de la Lumiere" (1678 г.) Хюйгенс показва как законът за синусите на Снел може да бъде обяснен или изведен от вълновата природа на светлината.
Въпроси и отговори
В: Какво представлява законът за пречупване на Снел?
О: Законът за пречупване на Снел е научен закон за пречупването на светлината или други вълни. В оптиката той гласи, че когато светлината преминава през различни материали, съотношението между синусите на ъглите на падане и пречупване не се променя.
Въпрос: Как може да се докаже законът на Снел?
О: Законът на Снел може да се докаже чрез принципа на Ферма, който гласи, че светлината се движи по пътя, който отнема най-малко време.
В: Какво представлява принципът на Ферма?
О: Принципът на Ферма гласи, че светлината се движи по път, който отнема най-малко време.
В: Какво представляват n и v в закона на Снел?
О: n е коефициентът на пречупване на средата, а v е скоростта на светлината в съответната среда (измерена в метри в секунда).
В: Какво представлява c в закона на Снел?
О: c представлява скоростта на светлината във вакуум, който има индекс на пречупване, равен на 1.
В: Как се изчислява скоростта, когато вълната преминава през материал с индекс на пречупване n?
О: Скоростта става c/n, когато вълната преминава през материал с индекс на пречупване n.
