Древна китайска музикална система: математика, честоти и пентатоники

Разкрийте древната китайска музикална система: математика зад честотите, монтаж на прагчета, пентатоники и практическо ръководство за 144 уникални тона.

Древната китайска музикална система се основава на много стара числова и акустична практика за определяне на тоновете. Тя използва прости дробни съотношения (най-често 3:2 и 4:3) за да получи интервали като перфектна квинта и кварта и след това при необходимост повтаря или намалява октавно (умножаване/деление по 2), за да вкара резултатите в обхвата на инструмента. Тази последователност от съотношения е известна в традицията като част от системата на 十二律 (двана́йсет лü) — дванадесетте основни звукови стъпки.

Практически пример за поставяне на прагчета

Най-лесно се обяснява с конкретен пример (както в текста по-долу):

• Направете дървена кутия с дължина 105 см и ширина 60 см. Поставете водачи (мостчета/маркировки) близо до всеки край така, че тези два водача да са на разстояние 99 cm един от друг — това ще бъде ефективната дължина на „отворената” струна.
• Умножете 99 cm по 2/3 → 66 cm. Поставете праг на тази позиция. (Съотношението 2/3 намалява дължината и повишава честотата в съответствие с обратната зависимост на честотата от дължината.)
• Умножете 66 cm по 4/3 → 88 cm. Поставете праг на тази позиция.
• Продължете последователно: 88 cm × 2/3 → 58,666... cm; 58,666... cm × 4/3 → 78,222... cm; 78,222... cm × 2/3 → 52,148... cm; 52,148... cm × 4/3 → 69,531... cm; 69,531... cm × 2/3 → 46,354... cm — което е твърде малко за тази дължина на кутията, затова го удвояваме (прибавяме една октава) до 92,708 cm и поставяме праг там.
• Продължавайте процеса (умножения по 4/3 и 2/3 и при нужда корекции с 2x или 1/2 за октави), докато не получите желания брой маркировки; в примера се поставят 11 прагчета.

Защо точно 2/3 и 4/3?

Съотношението 3:2 (или неговият еквивалент за дължини 2/3) дава перфектна квинта (интервал, широко използван в много музикални традиции). Съотношението 4:3 (дължина × 4/3) дава перфектна кварта. Чрез последователно прилагане на тези интервали и пренасянето в октави (умножение/деление по 2) се генерира цикъл от чисти интервали, който дава основата за дванадесетичната система на тоновете в традиционната китайска теория.

Пресмятане на честоти (пример с конкретна честота)

Честотата на струна е обратно пропорционална на нейната ефективна дължина (при еднакво натягане и маса на струната): f ∝ 1/L. Това означава, че ако отворената струна с дължина 99 cm е настроена на някаква базова честота, позиция на дължина 66 cm (2/3 от 99) ще даде честота 99/66 = 1.5 пъти по-висока. Например:

• Ако приемем, че отворената струна (99 cm) дава честота 440 херца, то позицията 66 cm ще произведе приблизително 440 × (99/66) = 440 × 1.5 = 660 Hz.
• Позицията 88 cm ще даде 440 × (99/88) ≈ 440 × 1.125 = 495 Hz.
• И т.н. — всяка позиция дава честота, която е множител на базовата, съответстващ на отношението между началната и новата дължина.

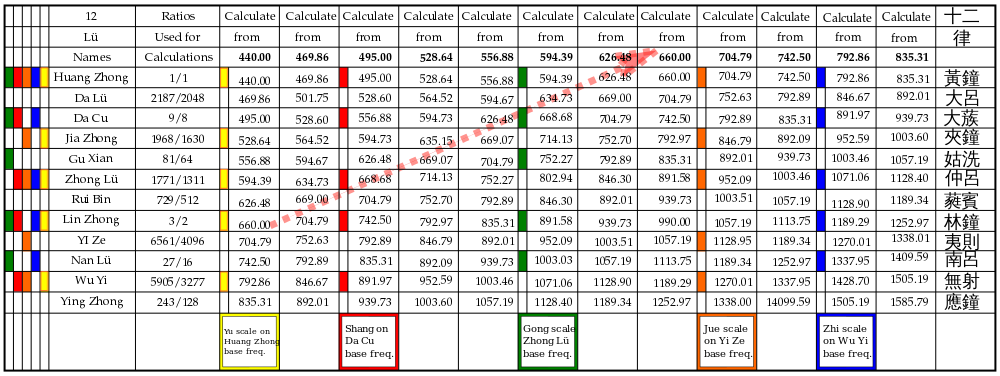
Така, като използвате тези прагове и спрямо отворената струна пресмятате честотите, за всяка „основна” струна можете да получите 12 характерни честоти (които формират колоната от 12 тона в описаната таблица). Ако имате 12 струни, настроени според процедурата, и прилагате всички тези позиции (премествайки пръсти или дръпвайки струните при различни прагове и без праг), в крайна сметка ще получите 144 измерими тона. Част от тях ще съвпадат октавно или по други чисти съотношения, но като цяло в тази система съвпаденията са по-рядко „равномерни” отколкото в днешната равномерно темперирана западна система.

От колоната към скалите

В текста се споменава таблица: след като изберете някаква референтна честота (например 440 херца — както е посочено), тя се умножава по определени съотношенията, за да се получи първата колона от честоти. Всяка от тези 12 честоти може да служи като „стартер” за своя собствена колона (т.е. да бъде начална тоналност за следваща серия от множители). Всяка колона съдържа 12 тона, от които можете да изберете:

• пет тона за пентатонична скала (пентатоника);
• или седем тона за хептатонична (напр. мажорна/минорна) скала.

Както е записано: „Всякакви пет честоти в колона могат да бъдат избрани, за да се направи пентатонична скала, стига да не са точно една до друга и да не са на повече от две разстояния една от друга.” Това означава, че при подбора се избягва вземането на две съседни степени (за да не се получат твърде тесни интервали) и се поддържа определена равномерност в разпределението на избраните пет тона, така че мелодичният материал да запази характерния за китайската музика пентатоничен вид.

Пентатоники и традиционни скали

В западната традиция младшите ученици учат седемстепенната мажорна скала с тонове „до, ре, ми, фа, сол, ла и ти” — и нейните лади, най-вече мажор и минор. В китайската традиция централно място заемат именно пентатоничните (петтонални) системи. Традиционно се различават пет основни пентатонични названия (в историческата терминология: 宮 gōng, 商 shāng, 角 jué, 徵 zhǐ, 羽 yǔ), които формират различни мелодични центрове и модалности. В практиката тези пет различни петтонални формули се използват за изграждане на мелодии и дават характерния „китайски” звук.

Разлики спрямо равномерно темпериране

Днешната западна равномерно темперирана (equal-tempered) система разделя октавата на 12 равни полутонa, така че всеки полутон е еднакъв множител. В древната китайска система, напротив, използваните дробни съотношения дават „чисти” интервали (прости дроби като 3:2, 4:3 и т.н.), което води до по-звучни (непосредствени, хармонично „чисти”) квинти и кварти в определени тоналности, но също така до неравномерни стъпки между съседните степени. Затова при прехвърляне на музика между системите някои интервали звучат различно и някои акорди/мелодични структури се променят.

Бележки и исторически контекст

Методите за маркиране на дължините и получаване на тоновете са приложими за различни инструментални семейства в Китай — например за гуджин (古琴), пипа, ерху и др. При гуджин има традиция на определяне на сигнатурни маркировки (hui), които често съответстват на подобни позиции. Историческите трактати и музиколози описват тези процедури още от античността, като подходът е бил както практичен (за строеж на инструменти), така и теоретичен (за дефиниране на ладове и концертни системи).

В резюме: описаният метод използва редуване на дробни множители (2/3 и 4/3) и октавни корекции, за да получи серия от позиционирани прагове; от тях се извеждат честоти (обратно пропорционални на дължините) и накрая — музикални скали (пентатоники и хептатоники). Този подход е различен от равномерното темпериране и придава специфично звучене и логика на традиционната китайска музика.

Въпроси и отговори

Въпрос: На какво се основава древната китайска музикална система?

Въпрос: Как се прави музикален инструмент, който може да свири всяка песен в древнокитайската система?

Въпрос: Какъв е примерът за хептатонична скала?

В: Колко различни гами използва традиционната китайска музика?

Въпрос: Пентатоничните гами обсъждани ли са в тази статия?

В: Каква честота е избрана за пример?

Въпрос: Колко честоти ще се получат, когато всички дванадесет струни се изсвирят в позиция на гриф и без гриф?

Търсене по буква